| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- IAM 사용자
- 백준
- 자바 2346
- BFS
- IAM Identity Center
- 백준 2346 자바
- 파이썬
- 10810 자바
- 2798 자바
- 자바 2164
- 코딩테스트
- 28278 스택 2
- 1010 자바
- 2164 자바
- 백준 28278 자바
- 백준 10866 자바
- 1764 자바
- 10813 자바
- 데보션영 3기
- 자바 1003
- 백준 1764 자바
- dfs
- 티움투어
- 자바
- 자바 28278
- 자바 10866
- 2346 풍선 터뜨리기
- 2748 자바
- 10807 자바
- 그리디
- Today
- Total
자두의 데브로그
[코테 스터디] Week3 정렬 개념 정리 본문
* 해당 포스팅은 아래 알고리즘 강의를 듣고 정리한 내용입니다.
https://www.youtube.com/watch?v=KGyK-pNvWos&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=4
정렬 알고리즘
정렬: 데이터를 특정 기준에 따라 순서대로 나열하는 것
→ 일반적으로 문제 상황에 따라서 적절한 정렬 알고리즘이 공식처럼 사용됨
ex. 데이터의 개수가 적을 때, 데이터의 개수가 많지만 데이터의 범위가 특정하게 한정되어있을 때, 이미 데이터가 정렬되어있을 때
컴퓨터에게 정확히 어떠한 방식으로 정렬을 수행할 것인지 코드를 사용해서 나타내어야 함
선택 정렬
처리되지 않은 데이터 중 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복
→ 매번 현재 범위에서 가장 작은 데이터 골라서 가장 앞으로 보냄
💡 선택 정렬 예시
7 5 9 0 3 1 6 2 4 8
[Step 0] 처리되지 않은 데이터(처음~끝) 중 가장 작은 ‘0’을 선택해 가장 앞의 ‘7’과 바꿈
0 5 9 7 3 1 6 2 4 8
[Step 1] 처리되지 않은 데이터(두번째~끝) 중 가장 작은 ‘1’을 선택해 가장 앞의 ‘5’와 바꿈
0(처리된 데이터) / 1 9 7 3 5 6 2 4 8
[Step 2] 처리되지 않은 데이터(세번째~끝) 중 가장 작은 ‘2’를 선택해 가장 앞의 ‘9’와 바꿈
0 1(처리된 데이터) / 2 7 3 5 6 9 4 8
.
.
.
정렬되지 않은 데이터 하나가 남았을 마지막 경우에는 자신의 위치와 동일해서 처리하지 않아도 된다.
0 1 2 3 4 5 6 7 8 9
탐색 범위는 탐색할 때마다 줄어들고, 매번 가장 작은 원소를 찾기 위해서 탐색 범위만큼 데이터를 하나씩 확인해야되기 때문에 매번 선형 탐색을 수행하는 것과 동일
⇒ 이중 반복문 사용
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(len(array)):
min_index = i # 가장 작은 원소의 인덱스
for j in range(i+1, len(array)): # 선형탐색 수행
if array[min_index] > array[j]: # 현재보다 더 작은 값이 있으면
min_index = j # 바꾸기 위해 min_index에 저장
array[i], array[min_index] = array[min_index], array[i] # 이를 통해 단순하게 swap 가능
print(array)
선택 정렬의 시간 복잡도
선택 정렬 = N번 만큼 가장 작은 수를 찾아서 맨 앞으로 보냄
구현 방식에 따라서 사소한 오차는 있을 수 있지만, 전체 연산 횟수는 아래와 같다.
N + (N-1) + (N-2) + . . . + 2 = (N^2 + N - 2)/2 = O(N^2)
삽입 정렬
처리 되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입 (데이터를 하나씩 확인하면서 데이터가 어느 위치에 들어가는 게 맞는지 적절한 위치에 들어가도록)
⇒ 선택 정렬에 비해 구현 난이도가 높은 편이지만, 더 빠르게 동작
💡 삽입 정렬 동작 예시
7 5 9 0 3 1 6 2 4 8
[Step 0] 첫 번째 데이터 ‘7’은 그 자체로 정렬이 되어 있다고 가정하고, 두 번째 데이터인 ‘5’가 어떤 위치로 들어갈지 판단. ‘7’의 왼쪽으로 들어가거나 오른쪽으로 들어가거나 두 경우만 존재
5 7 9 0 3 1 6 2 4 8
[Step 1] 이어서 ‘9’가 어떤 위치로 들어갈지 판단
5 7 9 0 3 1 6 2 4 8
[Step 2] 이어서 ‘0’이 어떤 위치로 들어갈지 판단
0 5 7 9 3 1 6 2 4 8
[Step 3] 이어서 ‘3’이 어떤 위치로 들어갈지 판단
0 3 5 7 9 1 6 2 4 8
.
.
.
0 1 2 3 4 5 6 7 8 9
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(1, len(array)):
for j in range(i, 0, -1): # 인덱스 i부터 1까지 1씩 감소하며 반복
# j는 현재 삽입하고자 하는 데이터의 위치
if array[j] < array[j-1]: # 한 칸씩 왼쪽으로 이동
array[j], array[i-1] = array[i-1], array[j]
else: # 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
break
print(array)삽입 정렬의 시간 복잡도
O(N^2): 선택정렬과 마찬가지로 반복문이 두 번 중첩되어 사용
But, 이중 for문이 사용된다고 해서 반드시 O(N^2)의 복잡도를 갖는 것은 아님!!
if) 반복문 안에 별도의 함수가 추가적으로 호출된다면 해당 함수도 고려해야함
→ 단순히 이중 반복문 안에서 비교 및 스와핑만 하기 때문에 O(N^2)
+ 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작
- 최선의 경우 O(N)의 시간 복잡도
- 💡 0 1 2 3 4 5 6 7 8 9
- 삽입 정렬 수행 시, 두 번째 원소부터 시작하여 들어갈 위치를 고르는데 바로 왼쪽에 있는 원소와 비교했을 때 본인이 더 커서 멈추면 되고, 세 번째도 동일, 오름차순 정렬을 수행할 때 이미 되어있다고 하면 탐색 과정이 바로 멈추기 때문에 왼쪽 데이터 중에서 자기가 어디로 들어갈지 고르는 부분이 상수 시간으로 대체되어 전체 정렬을 위한 시간 복잡도가 O(N)
퀵 정렬 (빠른 정렬 알고리즘 중 하나)
: 기준 데이터 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법
- (데이터의 특성과 상관없이 표준적으로 사용할 수 있는) 일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나
- 병합 정렬과 더불어 대부분의 프로그래밍 언어의 정렬 라이브러리의 근간이 되는 알고리즘
- 가장 기본적인 퀵 정렬은 첫 번째 데이터를 기준 데이터(Pivot)으로 설정
💡 퀵 정렬 동작 예시
5 7 9 0 3 1 6 2 4 8
[Step 0] 현재 피벗의 값은 ‘5’, 왼쪽에서부터 ‘5’보다 큰 데이터를 선택하므로 ‘7’이 선택되고, 오른쪽에서부터 ‘5’보다 작은 데이터를 선택하므로 ‘4’가 선택된다. 이 두 데이터의 위치를 서로 변경
5 4 9 0 3 1 6 2 7 8
[Step 1] 현재 피벗의 값은 ‘5’, 왼쪽에서부터 ‘5’보다 큰 데이터를 선택하므로 ‘9’가 선택되고, 오른쪽에서부터 ‘5’보다 작은 데이터를 선택하므로 ‘2’가 선택된다. 이 두 데이터의 위치를 서로 변경
5 4 2 0 3 1 6 9 7 8
[Step 2] 현재 피벗의 값은 ‘5’, 왼쪽에서부터 ‘5’보다 큰 데이터를 선택하므로 ‘6’이 선택되고, 오른쪽에서부터 ‘5’보다 작은 데이터를 선택하므로 ‘1’이 선택된다. 단, 이처럼 위치가 엇갈리는 경우 ‘피벗’과 ‘작은 데이터’의 위치를 서로 변경
1 4 2 0 3 5 6 9 7 8
[분할 완료] 이제 ‘5’의 왼쪽에 있는 데이터는 모두 5보다 작고, 오른쪽에 있는 데이터는 모두 ‘5’보다 크다는 특징, 이렇게 피벗을 기준으로 데이터 묶음을 나누는 작업을 분할(Divide = Partition)
1 4 2 0 3 / 5 / 6 9 7 8
[왼쪽 데이터 묶음 정렬] 왼쪽에 있는 데이터에 대해서 마찬가지로 정렬 수행
1 0 2 4 3
0 1 2 4 3
[오른쪽 데이터 묶음 정렬] 오른쪽에 있는 데이터에 대해서 마찬가지로 정렬 수행
→ 이러한 과정을 반복하면 전체 데이터에 대해서 정렬 수행
6 9 7 8
.
.
.
0 1 2 3 4 5 6 7 8 9
퀵 정렬이 빠른 이유: 직관적인 이해
이상적인 경우, 분할이 절반씩만 일어난다면 전체 연산 횟수로 O(NlogN)
✅ 너비 * 높이 = N * logN = NlogN
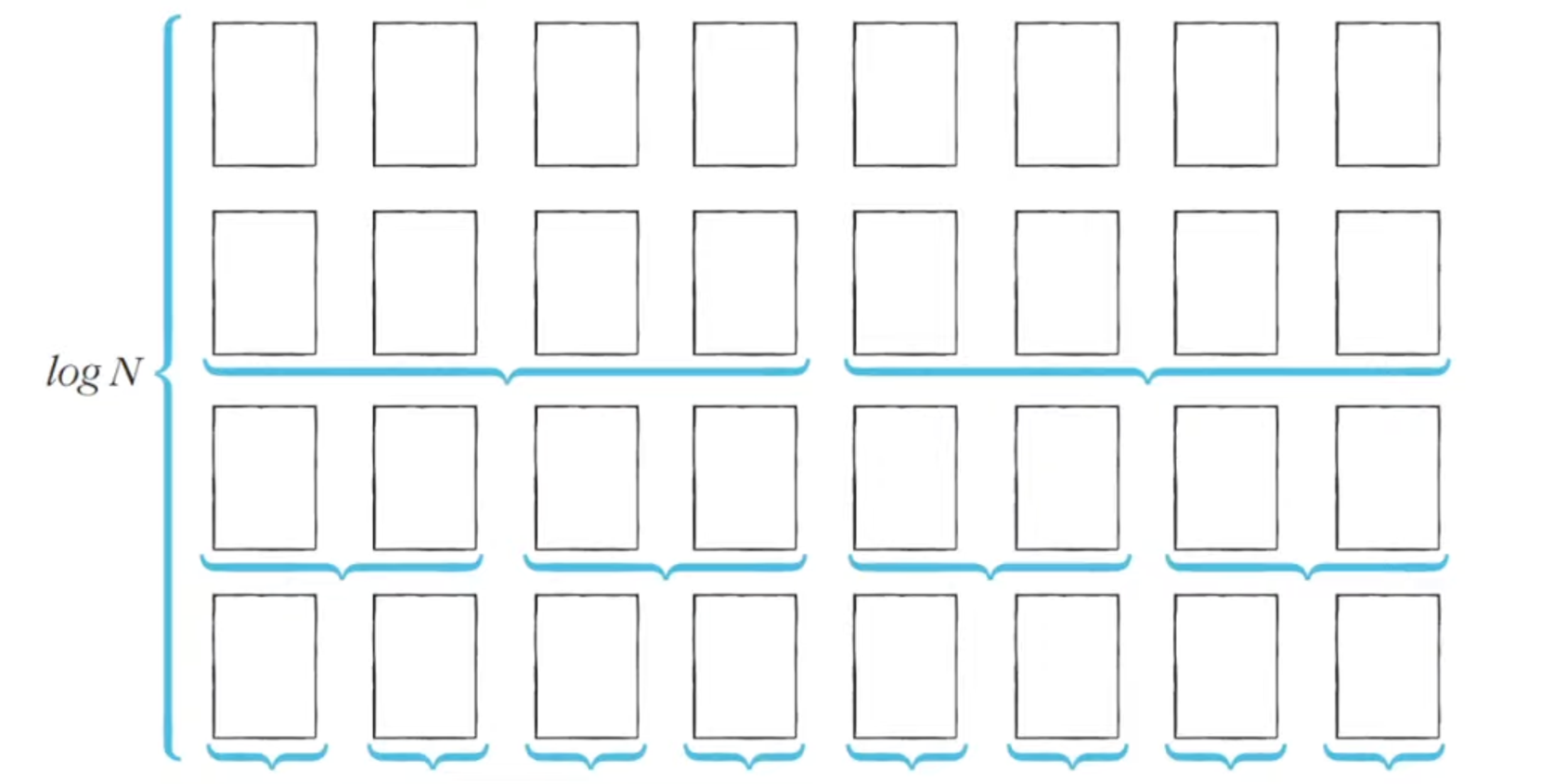
퀵 정렬의 시간 복잡도
평균의 경우: O(NlogN)
최악의 경우: O(N^2) (피벗 값에 따라 분할이 한 쪽 방향으로 편향된 경우)
ex. 이미 정렬된 배열에 대해서 첫 번째 원소를 피벗으로 삼는 경우: 본인의 자리에 본인의 값이 지정되고 자기 외의 값인 나머지 오른쪽 배열을 가지고 다시 분할
- 다양한 프로그래밍 언어에서 표준 정렬 라이브러리를 제공할 때 퀵정렬로 작성되어있다면 최악의 경우에도 O(NlogN)의 시간 복잡도가 나올 수 있도록 구현
⇒ 직접 구현 시, 최악은 N^2, 표준 라이브러리를 사용할 경우, NlogN
# 일반적인 코드
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start # 피벗은 첫 번째 원소
left = start + 1 # 피벗 바로 다음 원소부터
right = end # 가장 뒤부터
while(left <= right): # 엇갈릴 때까지 반복
# 피벗보다 큰 데이터를 찾을 때까지 반복
while(left <= end and array[left] <= array[pivot]):
left += 1
# 피벗보다 작은 데이터를 찾을 때까지 반복
while(right > start and array[right] >= array[pivot]):
right -=1
if(left > right): # 엇갈렸다면 right가 더 작은 값이니까
array[right], array[pivot] = array[pivot], array[right]
else:
array[left], array[right] = array[right], array[left]
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right - 1)
quick_sort(array, right + 1, end)
quick_sort(array, 0, len(array) - 1)
print(array)# 파이썬의 장점을 살린 방식의 코드
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
# 리스트가 하나 이하의 원소만 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array[0] # 피벗은 첫 번째 원소
tail = array[1:] # 피벗을 제외한 리스트
left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행하고, 전체 리스트 반환
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))계수 정렬
특정 조건이 부합할 때만 사용할 수 있지만 매우 빠르게 동작하는 정렬 알고리즘
→ 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용 가능
시간복잡도: 데이터의 개수가 N, 데이터(양수) 중 최댓값이 K일 때 최악의 경우에도 O(N+K) 보장
💡 계수 정렬 동작 예시
7 5 9 0 3 1 6 2 9 1 4 8 0 5 2
[Step 0] 가장 작은 데이터부터 가장 큰 데이터까지의 범위가 모두 담길 수 있도록 리스트를 생성
인덱스 0 1 2 3 4 5 6 7 8 9
개수(Count) 0 0 0 0 0 0 0 0 0 0
[Step 1] 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가
인덱스 0 1 2 3 4 5 6 7 8 9
개수(Count) 0 0 0 0 0 0 0 1 0 0
[Step 2] 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가
인덱스 0 1 2 3 4 5 6 7 8 9
개수(Count) 0 0 0 0 0 1 0 1 0 0
[Step 3] 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가
인덱스 0 1 2 3 4 5 6 7 8 9
개수(Count) 0 0 0 0 0 1 0 1 0 1
.
.
.
[Step 15] 결과적으로 최종 리스트에는 각 데이터가 몇 번씩 등장했는지 횟수가 기록됨
인덱스 0 1 2 3 4 5 6 7 8 9
개수(Count) 2 2 2 1 1 2 1 1 1 2
[Step 16] 결과를 확인할 때는 리스트의 첫 번째 데이터부터 하나씩 그 값만큼 반복하여 인덱스 출력
0 0 1 1 2 2 3 4 5 5 6 7 8 9 9
⇒ 공간 복잡도는 높지만, 조건만 만족한다면 매우 빠름
# 모든 원소의 값이 0보다 크거나 같다고 가정
array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
# 모든 범위를 포함하는 리스트 선언(모든 값은 0으로 초기화)
count = [0] * (max(array) + 1)
for i in range(len(array)):
count[array[i]] += 1 # 각 데이터에 해당하는 인덱스 값 증가
for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
for j in range(count[i]):
print(i, end =' ') # 띄어쓰기를 구분으로 등장한 횟수만큼 인덱스 출력계수 정렬의 복잡도 분석
시간/공간 복잡도: O(N+K) # 데이터의 개수만큼 데이터 체크(N, 첫 번째 for문) / 각 인덱스에 기록된 값만큼만 출력 수행(K: 원소 중 가장 큰 값) + 안쪽 반복문 전체 수행 횟수(N)
- 때에 따라서 심각한 비효율성을 초래할 수 있음
- 데이터가 0과 999999로 단 2개만 존재하는 경우 (공간을 백만까지 사용해야)
- 동일한 값을 가지는 데이터가 여러 개 등장할 때 효과적으로 사용 가능
- 성적의 경우(0~100), 100점을 맞은 학생이 여러 명일 수 있어 효과적
정렬 알고리즘 비교하기
+ 대부분의 프로그래밍 언어에서 지원하는 표준 정렬 라이브러리는 최악의 경우에도 O(NlogN) 보장
| 정렬 알고리즘 | 평균 시간 복잡도 | 공간 복잡도 | 특징 |
| 선택 정렬 | O(N^2) | O(N) | 아이디어가 매우 간단하다 |
| 삽입 정렬 | O(N^2) | O(N) | 데이터가 거의 정렬되어 있을 때는 가장 빠르다 |
| 퀵 정렬 | O(NlogN) | O(N) | 대부분의 경우에 가장 적합하며, 충분히 빠르다 |
| 계수 정렬 | O(N+K) | O(N+K) | 데이터의 크기가 한정되어 있는 경우에만 사용이 가능하지만 매우 빠르게 동작한다 |
예제 1) 두 배열의 원소 교체
핵심 아이디어: 매번 배열 A에서 가장 작은 원소를 골라서, 배열 B에서 가장 큰 원소와 교체
내가 푼 방법
- A를 오름차순으로 정렬
- B를 내림차순으로 정렬
- 동일한 인덱스에 해당하는 원소끼리 크기 비교를 해가며 최대 K번까지 값 변경
- 이때, 만약 a의 원소가 b의 원소보다 커진다면 더 이상 바꾸지 않음
- a에 해당하는 모든 값을 더함
⇒ 두 배열의 원소가 최대 100,000개까지 입력될 수 있으므로, 최악의 경우 O(NlogN)을 보장하는 정렬 알고리즘을 이용해야함
# 배열 A, B가 N개의 원소로 구성
# 최대 K번의 바꿔치기 연산 수행(A에 있는 원소와 B에 있는 원소 하나를 골라 서로 바꾸는 것)
# 최종 목표: A의 모든 원소 합이 최대가 되도록 하는 것
import sys
N, K = map(int, sys.stdin.readline().split())
a = list(map(int, sys.stdin.readline().split()))
b = list(map(int, sys.stdin.readline().split()))
a.sort()
b.sort(reverse=True)
# b = sorted(b, reverse=True)
for i in range(K):
if a[i] >= b[i]: # a의 가장 작은 수가 b의 가장 작은 수보다 작다면
break
else:
a[i], b[i] = b[i], a[i]
# sum = 0
# for i in a:
# sum += i
# print(sum)
print(sum(a)) # a의 합을 한 번에 구할 수 있음'코딩테스트 > 스터디' 카테고리의 다른 글
| [코테 스터디] 리스트의 모든 원소에서 같은 값 빼기 (0) | 2024.03.23 |
|---|---|
| [코테 스터디] sys.stdin.readline()으로 입력 받기 (0) | 2024.03.23 |
| [코테 스터디] Week4 이진 탐색 개념 정리 (1) | 2024.03.23 |
| [코테 스터디] Week2 DFS & BFS 개념 정리 (4) | 2024.03.14 |
| [코테 스터디] Week1 그리디 & 구현 개념 정리 (3) | 2024.03.09 |


