Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 28278 스택 2
- 2748 자바
- 10807 자바
- 백준 10866 자바
- 티움투어
- 10810 자바
- 백준 1764 자바
- 자바 1003
- 10813 자바
- 백준
- 2346 풍선 터뜨리기
- 2798 자바
- 데보션영 3기
- BFS
- IAM Identity Center
- 자바 28278
- 백준 28278 자바
- 파이썬
- 2164 자바
- dfs
- 자바 2346
- 그리디
- 자바 10866
- 1010 자바
- 자바 2164
- 자바
- IAM 사용자
- 코딩테스트
- 1764 자바
- 백준 2346 자바
Archives
- Today
- Total
자두의 데브로그
[자바] 백준 1735번 분수 합 본문
https://www.acmicpc.net/problem/1735
두 개의 분수를 입력한 다음 분수의 합을 구하는 문제였다. 여기서 특징은 기약분수를 구해야한다는 것이었는데! 어떻게 구현해야될지 고민하다가 max랑 min을 사용하여 분자와 분모 중 더 큰 수까지 나눠가면서 약수를 가진다면 나눠서 기약분수로 만들 수 있도록 구현하였다. 근데 풀고 보니 풀이 자체가 틀린 건 아니지만 너무 요상해서 다른 문제 풀이 방법을 좀 찾아봤다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
int c = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
int s = (a*d) + (b*c);
int p = (b*d);
int max = 0;
int min = 0;
if (s > p) {
max = s;
min = p;
}
else{
max = p;
min = s;
}
int i = 2;
while(i <= min){
if(max % i == 0 && min % i == 0){
min /= i;
max /= i;
i = 2;
}
else{
i++;
}
}
if (s > p) {
s = max;
p = min;
}
else{
p = max;
s = min;
}
bw.write(String.valueOf(s) + " " + String.valueOf(p));
bw.flush();
bw.close();
}
}
원래 이 문제의 의도는 유클리드 호제법을 사용하는 것이었다..!
유클리드 호제법 : 최대 공약수를 구하는 알고리즘
public static int gcd(int p, int q)
{
if (q == 0) return p;
return gcd(q, p % q);
}
이 알고리즘을 통해 최대 공약수를 손쉽게 구할 수 있다. 유클리드 호제법을 사용해 문제를 다시 풀어보자
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
int c = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
int s = (a*d) + (b*c);
int p = (b*d);
int gcd = gcd(s, p);
s /= gcd;
p /= gcd;
bw.write(String.valueOf(s) + " " + String.valueOf(p));
bw.flush();
bw.close();
}
public static int gcd(int p, int q){
if(q == 0) return p;
return gcd(q, p % q);
// ex. 4, 8 넣으면 gcd(4, 0) -> 4
}
}
p>q 라고 가정할 때, p % q = r 이라고 하면, p와 q의 최대 공약수는 q와 r의 최대 공약수와 같다. 이러한 공식을 따라서 계속 나머지를 구하는 과정을 반복하다가 나머지가 0이 되는 순간 나눠지는 수가 p와 q의 최대 공약수이다. 생각하면 이해가 되는데 또 생각하긴 어려우니까 일단 외워보자 ^^
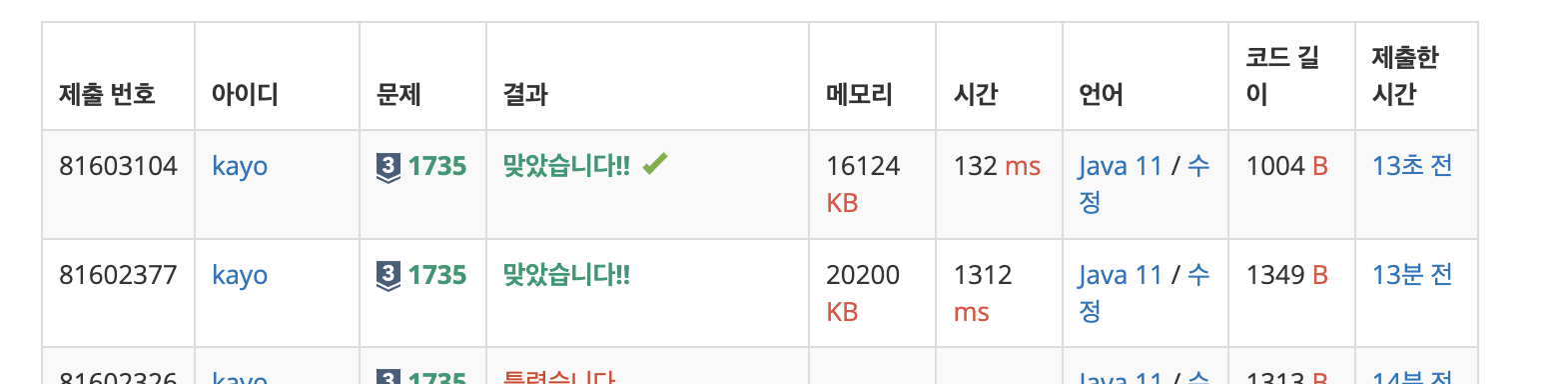
훨씬 간결하고, 시간 복잡도도 엄청 줄였다.
'코딩테스트 > Java' 카테고리의 다른 글
| [자바] 백준 24444번 알고리즘 수업 - 너비 우선 탐색 1 (0) | 2024.08.01 |
|---|---|
| [자바] 백준 24479 & 24480번 알고리즘 수업 - 깊이 우선 탐색 1 & 2 (1) | 2024.08.01 |
| [자바] 백준 19532번 수학은 비대면강의입니다 (1) | 2024.07.24 |
| [자바] 백준 2231번 분해합 (1) | 2024.07.23 |
| [자바] 백준 15649번 N과 M (1) (2) | 2024.07.22 |


